This stop on the maple Path looks rushed and scattered. Unlike the other resting spaces this one is barely a stop at all. There are some scattered sheets of paper and some strange looking wooden tiles in the shape of a hat.

Yesterday I got distracted 3d printing the new aperiodic tile on the block and playing the Diablo 4 beta so I didn't get the chance to post anything. So today I will summarize what I learned and potentially do a second post a little later.

Einstein Tiles

Earlier this week my brother Rain sent me a link to an article talking about a recent discovery of an aperiodic monotile called an Einstein tile. Along with the link, he demanded that I print "many of them in a bunch of colors so that I can pay with them". Naturally I jumped to it and ordered some color changing filament.

With a quick search online I found a 3d model of the tile that had a nifty curving path on top. The tile had the same design on the bottom though which I figured would cause some print quality issues, so I sliced it in half and sent it to my printer. It turns out this was a mistake.

I printed about 20 of the tiles all in the same orientation using the color changing filament but for the life of me I couldn't figure out how to get the tiles to fit together. No matter how I tried, there were always contradictions that made them fit poorly.

Digging a Little Deeper

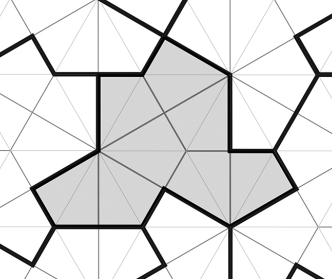
Eventually I realized that this monotile tiles infinitely only if you can flip the tile over. I later discovered by skimming the paper that the proof for the infinite tiling depends on constructing 4 different "meta tiles" out of the basic hat tile. They are as follows:

Of note is the triangle meta tile which is the only one which contains a reflected tile in the center. I didn't spend the time to fully understand the paper, but I think the proportion of standard tiles to reflected tiles is roughly 1 to 9 but I'm not positive.

With my new found knowledge, I printed a couple of the reflected tiles which enabled me to tile them all together.

Some Possible Improvements

Although I like the squiggly path over the tile I found online, I dislike that the pattern doesn't give any hints about how to properly construct the tiling. Ideally the pattern on the tile could help you hook up the larger tile combinations like the pinwheel and the larger triangle. Bonus points if the larger structure is revealed from the pattern.

To explain my thinking, its important to recognize the where the structure of the hat monotile comes from. It is a type of polygon called a polykite meaning its a shape constructed from smaller kites.

The path in the original model drew lines from the sides of the shape which corresponded with a long edge of one of the internal kites. This optimizes for thicker lines with more room to work with, but isn't ideal for revealing the meta tiles because the most important meta tile for the structure is the pinwheel one made of 6 standard tiles. They meet in the center with the short edges of the kite rather than the long edge.

If the paths between tiles joined the short edge, then that crucial point in the center would be highlighted because it would be a single tight circle where as the rest of the paths would meander at least a little bit before closing. The reflected tile could also contain a special pattern which has a similar circle in the center to highlight it's importance in the structure.

With those two reference points I imagine it would be much easier to construct the larger meta tiles and assemble them into a tiling of whatever size you would like. But for now I've left that as an exercise for some other time when I have patience enough to open some modeling software.

Till Tomorrow,
Kaylee